Применение User Defined Result из Ansys Workbench для обработки результатов на примере определения запаса прочности
Опция результатов User Defined Result обладает достаточно большим набором возможностей, позволяющих проводить обработку результатов с помощью арифметических операций, применять командны min, max, abs, вводить переменные и производить над ними вычисления. Конечно, общее число возможностей уступает командным вставкам на языке APDL, но позволяет в рамках своих возможностей быстро получить результат.
В данной статье приведены основные возможности данной опции и применение на примере определения запаса длительной прочности в зависимости от температуры.
Доступные стандартные переменные
Для задания отображения результатов используется поле Expression в опциях User Defined Result (пример). Набор отображаемых результатов соответствует набору результатов, доступных через команду *GET MAPDL (Mechanical Ansys Programming Design Language). Полный список доступных команд можно получить, нажав кнопку Worksheet панели меню Ansys при активном пункте Solution дерева проекта.
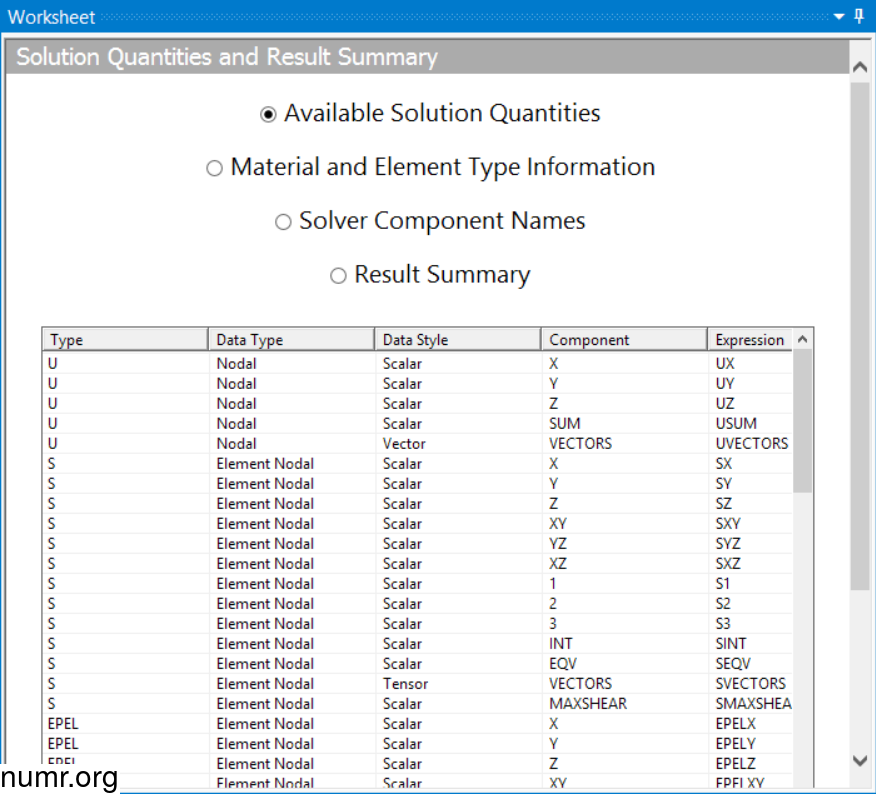
Для примера команды seqv, sx, s1 соответствуют получению результатов эквивалентных напряжений, напряжений по оси x и первых главных напряжений соответственно. Команды bfe, locz, dsum - температура, координаты узлов по оси z, суммарные перемещения соответственно.
Доступные операции и функции
Над всеми результатами произвольным образом можно применять арифметические операции, взятие значений по модулю, обрезка минимальных и максимальных полученных значений.
Перевод значений напряжений из МПа в кгс/мм2 (пример).
Максимальное значение из пары (пример).
Пользовательские переменные
Полученным результатам можно присвоить идентификатор и в дальнейшем вызывать их по этому идентификатору. Для этого предназначено поле Identifier (пример).
Определениие запаса прочности (пример)
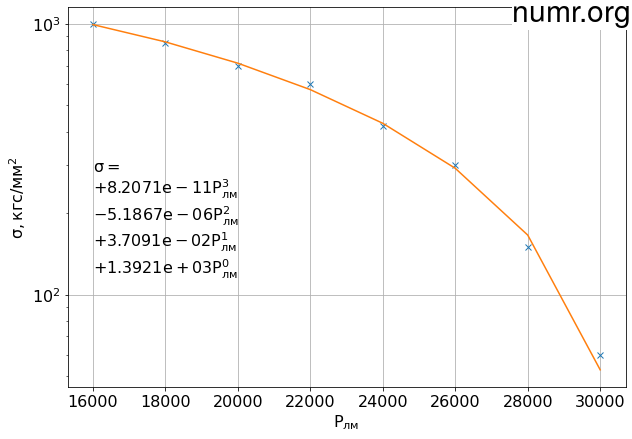
Запас длительной прочности будет определяться с помощью параметра Ларсона-Миллера Pлм. На рисунке приведена зависимость предела длительной прочности σдл от Pлм, где Pлм = Tτ + 20, T - абсолютная температура в Кельвинах, τ - длительность в часах.
Данную зависимость необходимо аппроксимировать подходящей функцией. В данном случае был выбран полином третьего порядка.
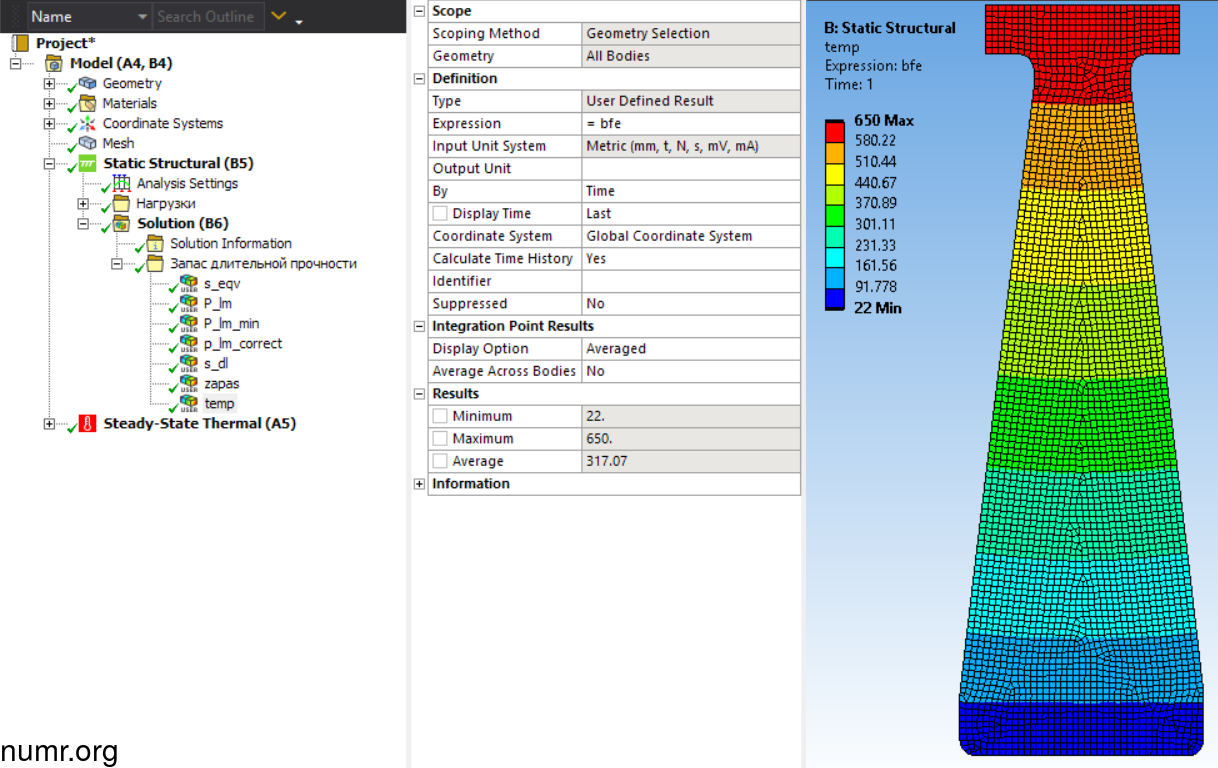
Отобразим распределение температуры с помощью команды bfe в поле Expression.
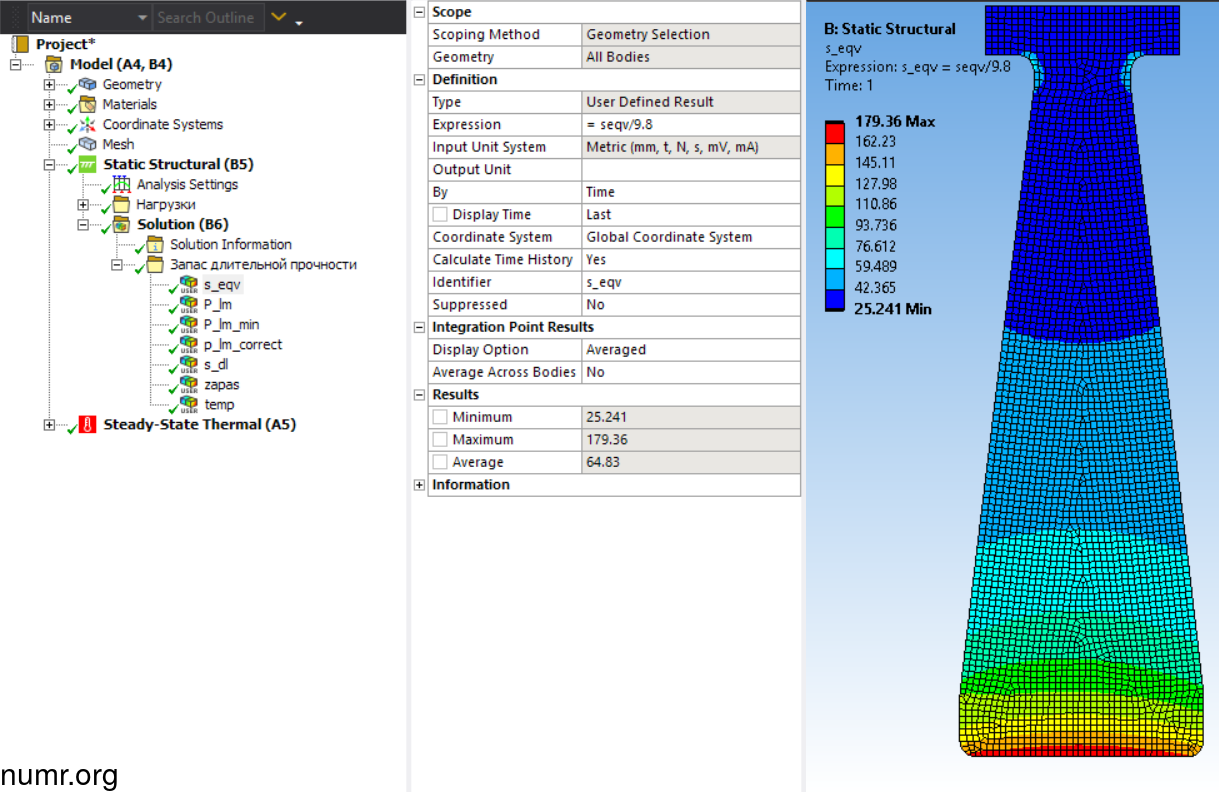
Переведем напряжения в МПа в кгс/мм2 с помощью команды seqv/9.8. В качестве идентификатора в поле Identifier введем s_eqv.
Теперь получим распределение параметра Ларсона-Миллера по объему детали c помощью выражения (273+bfe)*(log10(1000)+20), где 273 служит для перевода температуры из градусов Цельсия в Кельвин, 1000 - это длительность в часах, 20 - коэффициент, log10() - функция десятичного логарифма. В качестве идентификатора введем p_lm.
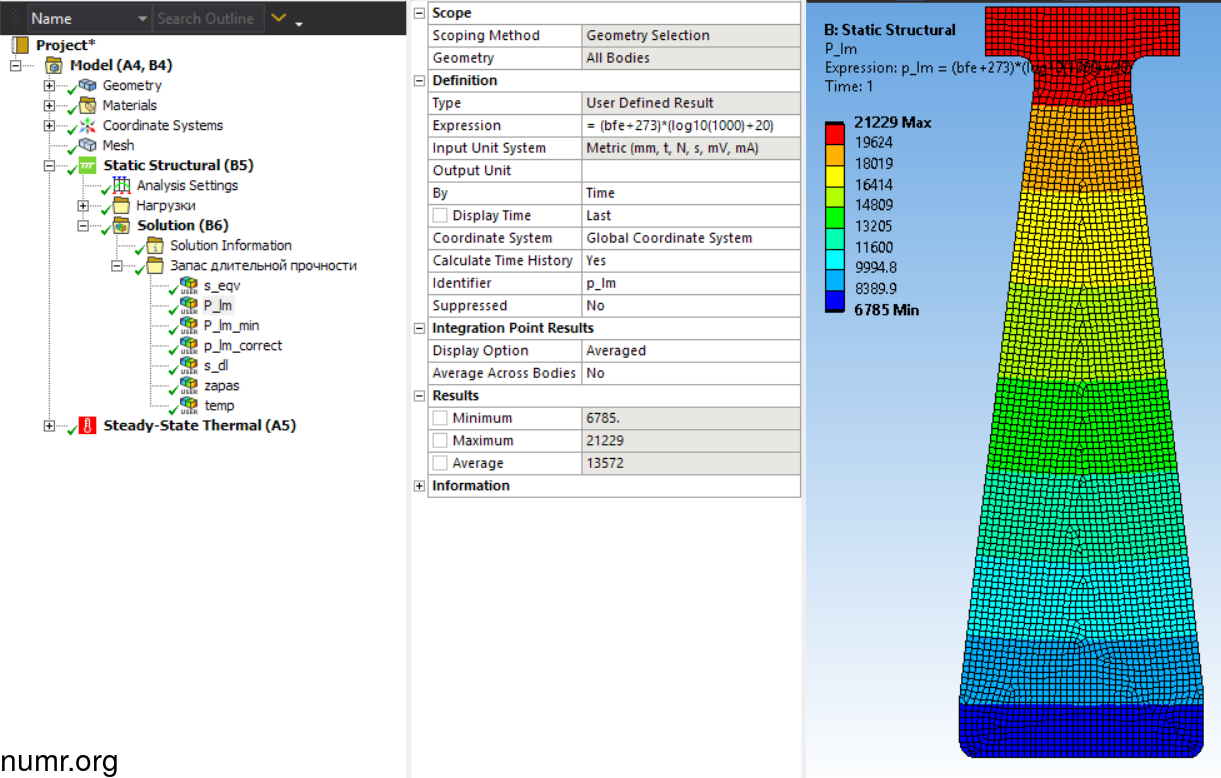
Как видно из вышеприведенного распределения существуют области с Pлм < 16000. Т.к. параметр Ларсона-Миллера определен в диапазоне от 16000 до 30000, то все полученные вне этого диапазона значения σдл будут некорректны. В качестве решения можно создать новое распределение, ограничив минимальное значение параметра Ларсона-Миллера 16000.
Для этого сначала создадим User Defined Result с полем Expression bfe-bfe+16000. Вместо bfe-bfe может быть любой другой параметр, он введен для того, чтобы получить распределение, равное 16000, иначе будет ошибка. В качестве идентификатора введем p_lm_lim.
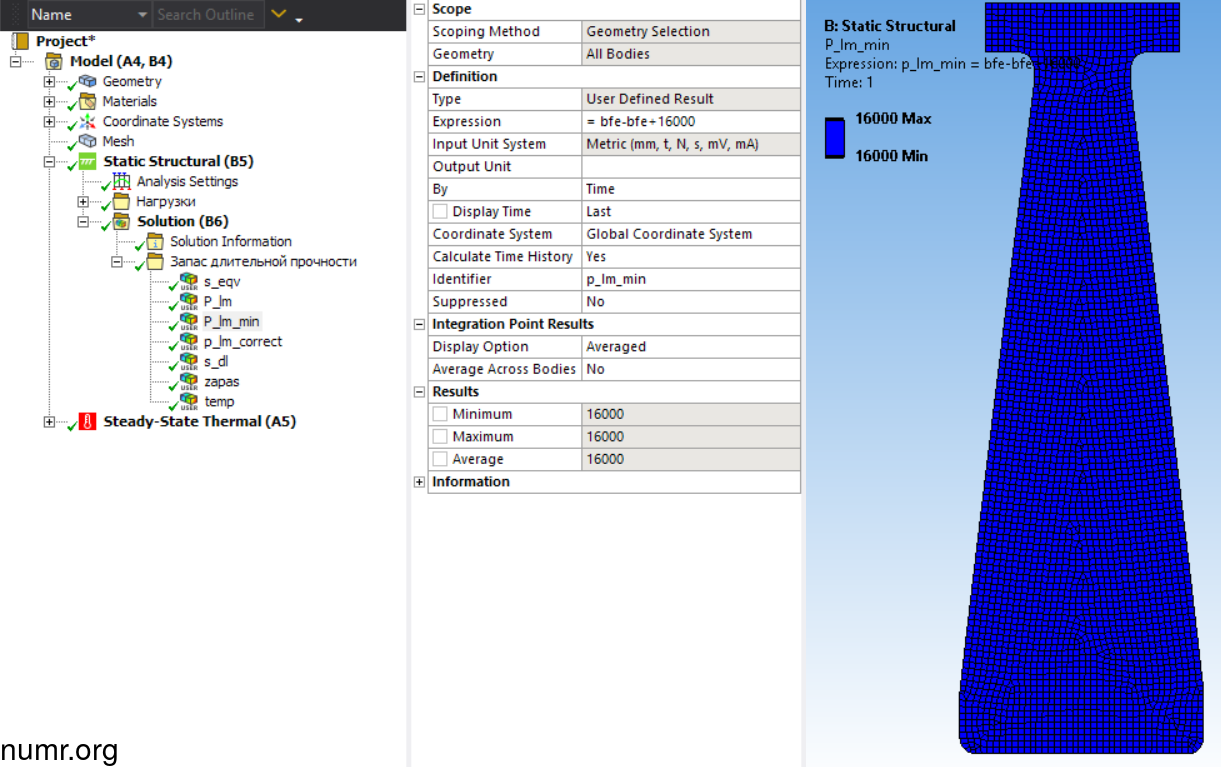
Теперь применим функцию max(), выбирающую максимальное из пары значений. В нашем случае она бует выглядеть так: max(p_lm, p_lm_lim). В качестве параметров выступают идентификаторы распределений, полученных ранее. Идентификатор примем p_lm_correct.
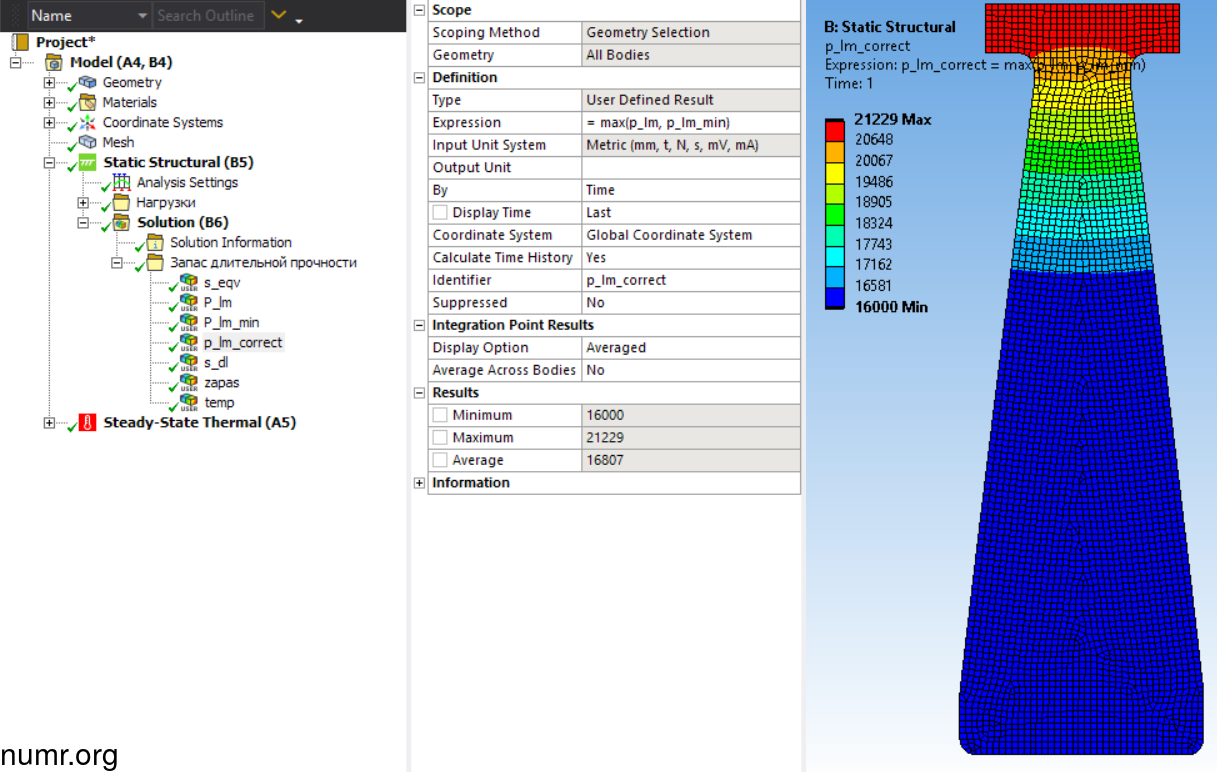
Теперь получим σдл по объему детали. Запишем полученную аппроксимационную функцию 8.2071e-11*p_lm_correct**3-5.1867e-06*p_lm_correct**2+3.7091e-02*p_lm_correct**1+1.3921e+03*p_lm_correct**0 в поле Expression и s_dl в поле Identifier.
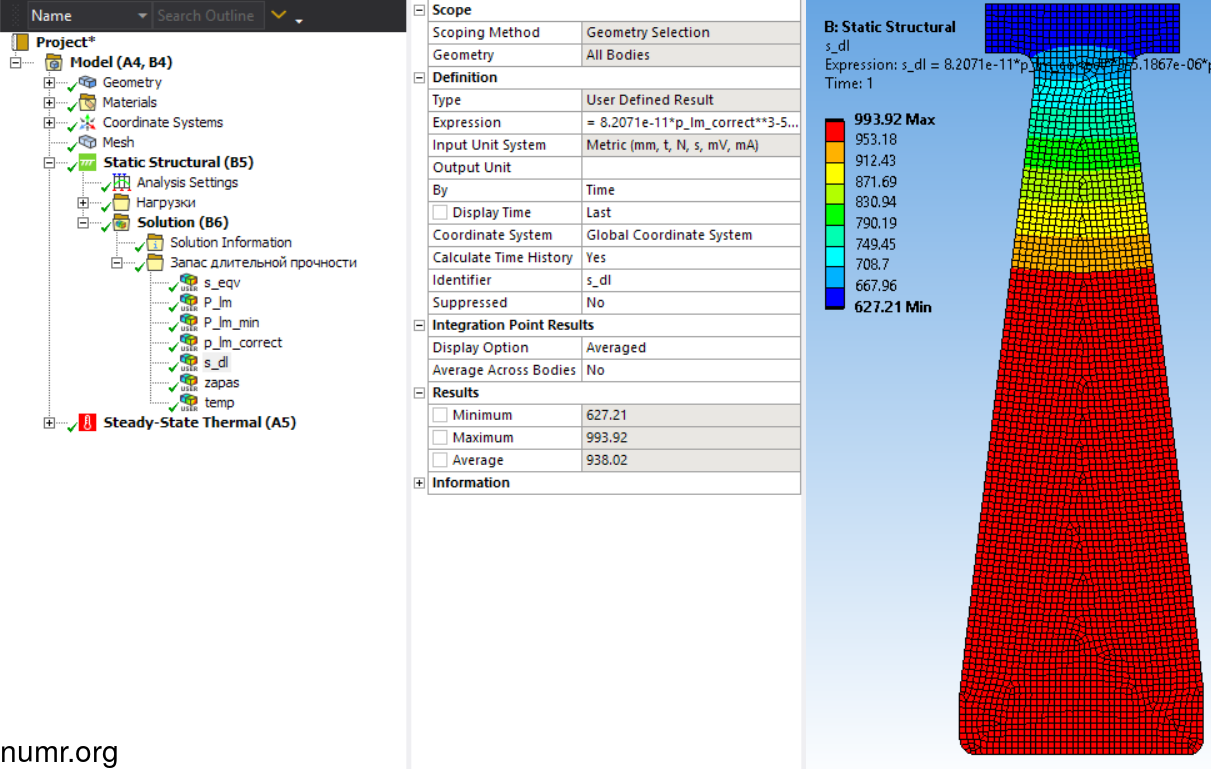
Отобразим запас прочности по длительным напряжениям s_dl/s_eqv.
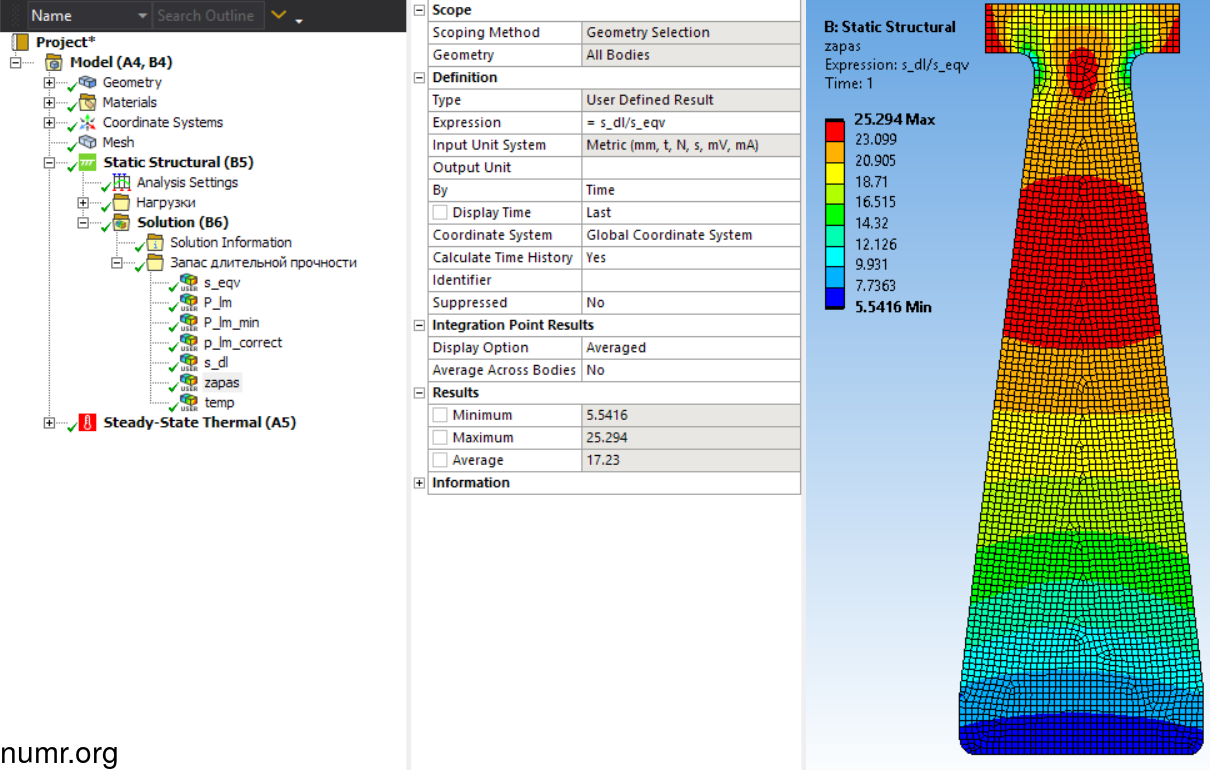
Выводы
User Defined Result позволяет не только отображать специфичные результаты на модели, но и производить над ними математические операции и совершать некоторую обработку.